A recent article on Scientific American has been finding some traction on Twitter, and it talks about some recent research on how to optimize difficulty to maximize learning. The paper in question is still under review, but a preprint copy can be found here.

Why I like this paper
Well, let’s start with the basics: making an assessment that appropriately challenges students is tough. I perceive lots of disagreement in the education world on this question, also. While teaching AP Biology I have been in all places on the spectrum…
- Brutally difficult – we put up some incredible numbers, but I ran off a great many students who could not meet such lofty expectations.
- Overly forgiving – I made assessments intended to be aced. I had students feeling great and earning top marks in the class, only to earn middling scores on the AP exam.
For all the opinions on how difficult AP (and AP Biology in particular) should be, I rarely see much research referenced on the topic. There’s TONS of data collected on whether the AP score is a good measurement (we actually chatted with Abby Whitbeck from the College Board recently… they know their stuff). That’s not the same thing as asking whether the thing we can measure with high confidence is actually the mark we should be measuring.

It’s not particularly controversial to say that there is such a thing as an exam that is too difficult. It’s also a compelling thought experiment to stop and imagine what your real reaction would be if every student returned a 100% on your next exam. Think about it!
- How was there such rampant plagiarism?
- Did the exam get compromised?
- Did I write the exam too easy?
- Are the questions reliable indicators of mastery?
This paper adds some formalized, systematized thinking to the notion that there is a sweet spot for exams. Yes, this was a simplified system (very common in research)… but if your exam includes a meaningful amount of multiple choice questions, you’re not too far off from dichotomous choice. Is EVERY distractor equally compelling…
What does it mean (or not mean)?
There are limits to applicability, especially if you AREN’T using multiple choice assessments (in which case, the study only applies in the most abstract sense). What it does say is that there is a curve to describe the learning value of tasks. Neither extreme is optimal, and I think that jives with most teachers’ intuition. Desirable difficulty is a target for which we shoot.
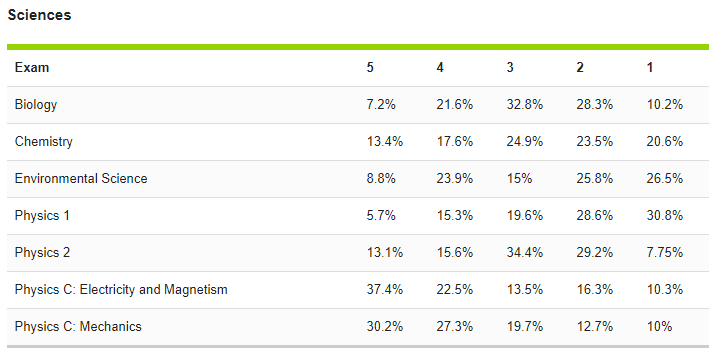
I have minimal stake in what a 5 should mean anymore, but I will note that an A in introductory university biology is more common than 7%… What matters (and I tweeted as much) here is that some teachers model their classroom assessments off the AP exam. When that becomes true, I think this ‘elites only’ attitude becomes really dangerous.
Granted, that’s a major assumption. It’s actually the assumption I am most interested in discussing… but the Twitter thread didn’t really go that way. I’ll just plant my flag, for the record: if the AP exam 5 is going to be as rare as it is, pinning your classroom assessments to the AP exam is going to exclude students we shouldn’t exclude.
And yes, please @ me on that.
I’m just going to disagree with you here. We use models in research all the time, including education. The authors explicitly make the connection themselves in the last sentence of the abstract:
” We demonstrate the efficacy of this ‘Eighty Five Percent Rule’ for artificial neural networks used in AI and biologically plausible neural networks thought to describe human and animal learning “
There are limits to how well the knowledge will transfer, but I think it is a mistake to dismiss transfer out-of-hand.
So that’s what I’ve got. Is this paper the new gospel on assessment? No, of course not. I’ll like it a lot more once it actually publishes. I do think it gives a compelling mathematical treatment to a topic that too many educators try to do with intuition alone.
But most of all… I like to talk about it. I am eager to correct my errors and learn from your responses.
If you’re going to @ me, make it to @RalphCSTEM.
